
In part 1 I proposed a simple modification to Google’s Multi-Window Multi-Burn Rate alerting setup and I showed how this modification addresses the cases of varying-traffic services and typical latency SLOs.
While my proposed solution was simply to alert on the error budget instead of the error rate, in this part I will show how we can still alert on the error rate but do it correctly. More importantly, the novel error-rate-based alert I will develop will expose a dynamic time-dependent burn rate expression which in contrast to Google’s static one leads to built-in compatibility to varying-traffic services.
Motivation
A certain disadvantage in my proposed solution in part 1 is that the metric which it alert on is the error budget while the metrics we care for when implementing SRE are the SLIs (or the actual error rate) and the percentage of error budget consumption. Hence, alerting on the error budget might not be consistent with our SLO and percentage of error budget consumption dashboards.
Again, the solution for this is quite easy. Eventually, the alert rule is just inequality between the actual number of bad requests in the alerting time window to some multiple of the error budget (defined by the percentage of error budget consumption that we want to alert on). If we divide this inequality by the total number of requests in the alerting time window we will get the desired inequality rule for an error-rate-based alert.
But, wait… isn’t it what Google did in the first place? Why do we need to go back and forth from error budget to error rate? To answer these questions, I’ll show in the following how Google’s formulation of static burn rate inevitably leads to an overly strict assumption on the traffic profile that doesn’t hold for varying-traffic services and how a correct transformation from the error budget domain to the error rate one leads to the more generalized form of time-dependent burn rate which is compatible with all traffic profiles.
Notations
To ease with the mathematical formulations let us define the following notations:
- wₐ - Alert time window (for example 1h, 6 h, etc.)
- w_slo - SLO period (7 days, 28 days, etc.)
- Nₐ(t) - Total number of events in the alert time window, wₐ
- Nb(t) - Total number of bad events in the alert time window, wₐ
- N_slo(t) - Total number of events in the SLO period, w_slo
- EB(t) - Error budget. The allowable number of bad events for the SLO period, w_slo
- EBP_t - The percentage of error budget consumption used as a threshold for alerting
- SLO - The SLO defined on the SLO period, w_slo. expressed as fraction (0.99, 0.999, etc.)
- ER_slo - The allowable error rate for the SLO window, w_slo: 1-SLO
- ER(t) - The actual error rate calculated on the alert time window, wₐ:
- BR - The static burn rate as defined in chapter 5 of Google’s SRE workbook:
where (t) denotes time-dependent variables.
Why Static Burn Rate Is Wrong?
The starting point in Google’s solution is a percentage of error budget consumption that we want to alert on, given the alert time window. That means that the alerting rule we should originate from is:
However, since the natural choice is to alert on the error rate and in order to transform the defined percentage of error budget consumption to error rate threshold, Google used the aforementioned definition of burn rate to give the following alerting rule:
Substituting the error rate and burn rate terms with their aforementioned definitions into the above expression gives:
and by multiplying the above expression with Nₐ(t) / EB(t) we get:
Comparing the right-side of this expression with the right-side of the percentage-of-error-budget alerting rule above leads to the following equation:
which we can develop to the following result:
and this is exactly the root cause for the incompatibility of Google’s alerting solution to varying-traffic services: The burn-rate-based alerting rule of Google holds only when the total number of events in the alerting time window is equal to the average number of events for this window along the SLO period. In all other cases, reaching the burn-rate threshold doesn’t mean that we reach the percentage-of-error-budget threshold that we aim for in the first place…
Time-Dependent Burn Rate
As mentioned above the remedy is to formulate the error-rate-based alert directly from the percentage-of-error-budget-based alert rule as follows. As we already saw, the alert rule on the percentage of error budget consumption is:
Multiplying the above expression by EB(t)/Nₐ(t) gives:
The left side is by definition the error rate, ER(t), and the error budget term can be expressed as multiplication of the SLO error rate and the total number of events in the SLO period:
and just by rearranging the terms on the right side, we get the desired alert rule:
where we can immediately notice the new time-dependent burn-rate term:
where the constant ratio between the SLO period to the alerting time window has been replaced by the more favorable time-dependent ratio between the total number of events in the SLO period to the total number of events in the alerting time window.
To illustrate the importance of using dynamic burn rate I used a web traffic dataset from Kaggle, “Example web traffic” with typical varying-traffic: low traffic at nights and high traffic during the day, and plot the traffic against the dynamic burn rate and the static one as a reference, as shown in the figure below:
As expected, the dynamic burn rate change significantly over time as a function of the number of requests (hits): It is high at low traffic hours so only a high error rate will cause the alert to fire and vice versa at high-traffic hours. This is exactly the desired behavior we seek to obtain fixed error budget consumption alerts. It can also be seen that the difference between the dynamic to the static burn rate can reach up to two orders of magnitude, which emphasizes how unsuitable the static threshold is to be used for alerting on a fixed percentage of error budget consumption.
We can also extend this observation by extracting the “actual (wrong) error budget consumption threshold” which is obtained when the static burn rate is used:
where:
is this actual error budget consumption threshold. Notice again how this term is equal to the fixed error budget consumption target only when the ratio between the total events in the SLO period to the total events in the alerting time window is equal to the constant ratio between the SLO period to the alerting time window. If we plot it we will get:
This figure also emphasizes the incompatibility of the static burn rate to varying-traffic services, where we eventually alert on different error budget consumptions each hour: in low-traffic hours on low ones, hence decreasing the precision, and in high-traffic hours on high ones, hence decreasing the recall. Moreover, the third pick demonstrates how in cases of an unusual increase in the traffic volume the miss becomes much more significant: In our case, the alert will fire only if we already consumed ~27% of the error budget…
3rd Option: Alert on Percentage of Error Budget
So far we discussed error-budget-based (in part 1) and error-rate-based alerting setups (in this part). Notice that those two setups have non-constant terms in the threshold expression: In the error-budget-based alert this is N_slo(t) and in the error-rate-based alert these are N_slo(t) and Nₐ(t). For those who will argue that these kinds of dynamic thresholds can be confusing or misleading, there is a third option (or maybe this is the first natural option).
Since both of the above setups derived from the fixed threshold on the percentage of error budget, why not alert directly on this percentage? Recall the alert rule on the percentage of error budget consumption is:
From here we can immediately get the final alert expression as:
Notice that all three alerting options are equivalent: All of them will fire when we cross over the defined percentage of error budget threshold. In fact, the above 3rd one is obtained by dividing both sides of the 1st one, the error-budget alert expression, by ER_slo x N_slo(t).
The nice thing this alert expression reveals to us is that we actually don’t care about the total number of events in the alerting window. The only influential metrics are the total number of bad events in the alerting window and the total number of events in the SLO period. This is directly due to the definition of the percentage of error budget consumption as our starting point for the alert. Since this percentage is defined on the whole SLO period, the total number of events in the alert time window shouldn’t influence it.
Computational Considerations
Since all the three options of alerting on the error budget consumption require up-to-date measuring of the total number of events in the SLO period, it may be computationally heavy. However, since this metric changes slowly over time we don’t necessarily have to measure it as frequently as the other metrics. Instead, we can sample it once a day and it should be enough. To validate it I resampled the calculated rolling N_slo(t):
As we can see there is no significant difference between the true burn rate to the approximated one. Even when the difference between the actual N_slo(t) to the resampled one is relatively large, as there is on 21/10/2017, its influence on the burn rate is negligible. We can validate this observation by calculating the log of the accuracy ratio:
which results in only 0.008.
Conclusion
In part 1 of this post, I introduced the incompatibility of Google’s Multi-Window Multi-Burn Rate alerting setup to varying-traffic services and/ or relative low SLOs. As a proposed solution I presented the 1st of three alternatives to this setup which is to alert on the error budget.
To strengthen the above argument, in this part, I showed mathematically why Google’s alerting setup can not fit the case of varying-traffic services. Additionally, I presented two more alternatives, equivalent to the first one, hence also compatible with the scenario of varying-traffic services. To summarize and by using the aforementioned notations, those 3 alternatives are:
- Error-Budget-Based Alert:
2. Error-Rate-Based Alert:
3. Percentage-of-Error-Budget-Based Alert:
where it is easy to notice the equivalence that exists between the above expressions.
I hope you will find this post, in its two parts, helpful for alerting on your SLOs.
Start blogging about your favorite technologies, reach more readers and earn rewards!
Join other developers and claim your FAUN account now!
User Popularity
44
Influence
4k
Total Hits
2
Posts









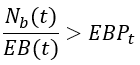
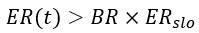

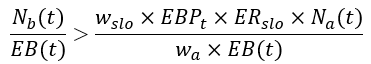

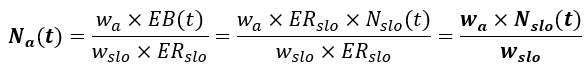

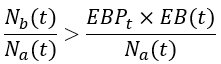
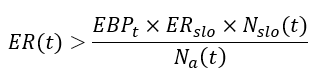

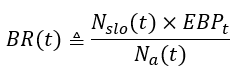









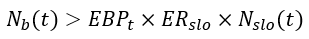
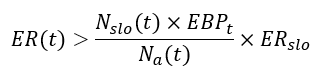








Only registered users can post comments. Please, login or signup.