Graph-Data Structure

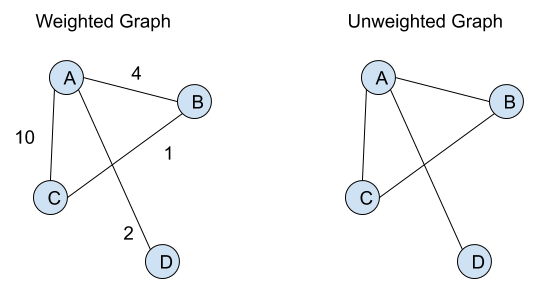
A Graph is a non-linear data structure that consists of nodes and edges. The nodes are sometimes referred to as vertices and edges are the lines that connect any two nodes or vertices in the graph.

A more technical definition could be :
“ A Graph is a pair of sets. G = (V,E). V is the set of vertices. E is a set of edges. E is made up of pairs of elements from V (unordered pair)”

Graphs are used to solve many real-life problems. Graphs are used to represent networks. The networks may include paths in a city or telephone network or circuit network. Graphs are also used in social networks like LinkedIn, Facebook.

Graph Terminology

• Path: It is the sequence of vertices in which each pair of successive vertices is connected by an edge.
• Cycle: It is a path that starts and ends on the same vertex.
• Simple Path: It is a path that does not cross itself that is, no vertex is repeated (except the first and the last). Also, simple paths do not contain cycles.
• Length of a Path: It is the number of edges in the path. Sometimes it’s the sum of weights of the edges also in case of weighted graphs.
• Degree of a Vertex: It is the number of edges that are incident to the vertex.

Now when we have understood about what graph data structure is and it’s terminology, so let’s move ahead and see how we can represent graphs.

Graph and its representations

A graph is a data structure that consists of the following two components:

1. A finite set of vertices also called as nodes.
   2. A finite set of ordered pair of the form (u, v) called as edge. The pair is ordered because (u, v) is not the same as (v, u) in case of a directed graph(di-graph). The pair of the form (u, v) indicates that there is an edge from vertex u to vertex v. The edges may contain weight/value/cost.

The following two are the most commonly used representations of a graph.
1. Adjacency Matrix
2. Adjacency List
There are other representations also like, Incidence Matrix and Incidence List. The choice of graph representation is situation-specific. It totally depends on the type of operations to be performed and ease of use.

Adjacency Matrix:
Adjacency Matrix is a 2D array of size V x V where V is the number of vertices in a graph. Let the 2D array be adj[][], a slot adj[i][j] = 1 indicates that there is an edge from vertex i to vertex j. Adjacency matrix for undirected graph is always symmetric. Adjacency Matrix is also used to represent weighted graphs. If adj[i][j] = w, then there is an edge from vertex i to vertex j with weight w.

The adjacency matrix for the above example graph is:

Pros: Representation is easier to implement and follow. Removing an edge takes O(1) time.

Cons: Consumes more space O(N²). Even if the graph is sparse(contains less number of edges), it consumes the same space.

Types of Graph

Following are the different types of graph:

• Weighted Graph

Weighted graph is a graph in which edges have a weight. So when I say edges have a weight, what I mean to say is that they have some numbers which typically shows the cost of traversing in a graph. When we are concerned with the minimum cost of traversing the graph then what we do is we find the path that has the least sum of those weights.

Example: weights can be the distances between cities or can be the fare of travelling.

Example of a Weighted Graph

• Unweighted Graph

Unweighted graph is a graph in which edges have no weight. In such a case, edges simply show connections.

Example: edges can show the path or route between cities.

Example of a Unweighted Graph

• Undirected Graph

These type of graphs have no implied direction on edges between the nodes. Edge can be traversed in either direction.

Example of a Undirected Graph

• Null Graph

A graph is known as a null graph if there are no edges in the graph.

• Trivial Graph

Graph having only a single vertex, it is also the smallest graph possible.

• Regular Graph

The graph in which the degree of every vertex is equal to the other vertices of the graph. Let the degree of each vertex be K then the graph

• Complete Graph

The graph in which from each node there is an edge to each other node.

Tree v/s Graph

Trees are the restricted types of graphs, just with some more rules. Every tree will always be a graph but not all graphs will be trees. Linked List ,Trees and Heaps all are special cases of graphs.

I hope this blog gives you a clear understanding about graphs in data structures. If this blog helps you understand the concept so share it with your friends and feel free to share your views and drop feedback about the blog.
And stay connected to know about more data structures.