Recursion Simplified

This is basically a way of taking complex problems and breaking them down to the simplest form.

In recursion we always have the base and recursive case;

The base case refers to the simplest instance of the problem; ie; sum([]) = 0, which means we can sum/add nothing, we down to our simplest form.

Now, what is a recursive case? think of this as a big problem that needs to be shrunk to the simplest form.

Using the sum example; sum 1([2,3,7]) and sum 2([2,3]) has sum([2,3]) as a repeating value, simplicity is king in the world of programming, with the aim of making progress to the base case.

Let us jump to examples, were we will tackle the factorial problem, the recursion problem and the Tower of Hanoi problem.

The Factorial Problem

Let’s write a function “fact” that takes in a number as an argument and returns the factorial of that number.

factorial works as follows; the factorial of ’n’ is the product of all positive numbers from 1 to ’n’ example:

factorial (7) = 5040 = 7*6*5*4*3*2*1

factorial (6) = 720 = 6*5*4*3*2*1

factorial(5) = 120 = 5*4*3*2*1

factorial(4) = 24 = 4*3*2*1

factorial(3) = 6 = 3*2*1

factorial(2) = 2 = 2*1

factorial(1) =1

Immediately we can identify our base case which is factorial of 1, factorial(1) needs no further computation/calculation .

Looking at the above expressions, we can see factorial(7) is our biggest problem with all those numbers and computations that have to happen, hence we need to break it down.

When studying the expressions you immediately see the overlapping, ie; Factorial(7) has 6*5*4*3*2*1 and factorial(6) has 6*5*4*3*2*1, this is a repetition, wouldn’t it be better if we write it as follows; factorial(7) =7*factorial(6).

Same is applicable with factorial(6) and factorial(5), we can simply say factorial(6)=6* factorial(5).

lets move on to factorial(5) and simplify it as factorial(5)=5*factorial(4).

factorial(4)=4*factorial(3) and factorial(3) can be expressed as 3*factorial(2) until we get to our base case which is factorial(1).

So we can generalize this as factorial(n) = n*factorial(n-1), this means the factorial of whatever value (n)is n times the factorial of 1 less.

The above expressions can also be written as;

factorial of 7 can also be written as 7!=7*6!, with the symbol ! representing factorial.

6!=6*5!

5!=5*4!

4!=4*3!

3!=3*2!

2!=2*1!

1!=1

Thus our recursive case is factorial(n) = n*factorial(n-1), this recursive case will eventually lead us to 1, which is the base case.

let's illustrate this in Python;

We have our function which is called fact and will take in n(n being the value, could be 7,5,6 depends so we just name it n.

We want it to return n(the value) and factorial of n(a value) less than one, we can immediately observe that by reducing our value by one we are simplifying the problem.

The same pattern will be applicable as we solve The Tower of Hanoi problem and Fibonacci sequence.

First and foremost we need a base case, which will limit our function from calling itself, an infinite amount of times.

Then we need to check if the number is zero(0), if n is 0 then we can return 1, as the factorial of 0 is 1.

Time to instruct our Python interpreter to create a function named fact, and to check for a base case, if our base case is zero then return 1, else return our recursive case which is n*fact(n-1). Our output matches what we had calculated manually.

The Tower Of Hanoi

Moving on to our next problem, which is a popular mathematics game/quiz.

Rules to the game are simple; the number of moves is 2*n-1, n represents the number of disks and in our case, we have 4 disks. You cannot place a disk that is larger on top of a disk that is smaller. Our goal is to move all of the disks to c(which is our goal).

We can definitely use recursion for this problem, we can move 3 disks(the green, purple and blue simultaneously to b, which is the middle. Remember one of the principles of recursion is less 1, (n-1).

Then we can move the red disk which is the largest disk to our goal, which is C, then after that move the green, purple and blue to our target.

We took a complex problem of 4 disks, applied recursion and reduced one disk and we were able to simplify our problem, this is applicable to any number of disks.

Let’s write Python code for this;

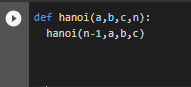
Starting off with the function hanoi, which takes in a,b,c; a being the start, b being the auxiliary, c our target and n is the number of disks.

Now we first want to move n-1, so 4–1 which gives us 3 disks to move which are the green, purple and blue disks.

Moving on to the large disk, and changing its position from a to c.

And finally, we need to move the n-1(3) disks from b which is our auxiliary to our target c.

But we also need a base case, or the hanoi function will call itself infinitely until we get an error, so we have 0 as our base case, no disks nothing.

In the code above we are telling Python to check for the base case, a check if there are any disks, if not, do nothing, but if they are, perform the recursive function.

Fibonacci Problem

Moving on let's solve the Fibonacci problem using recursion.

We want to write a function to return the nth term of the Fibonacci sequence, well what is the Fibonacci sequence?

1,1,2,3,5,8,13,21

Here is how the sequence is constructed;

The first two terms are 1’s, then after each term is the sum of the previous two terms.

1+1 = 2 this is the 3rd term

1+2 = 3 is the 4th term

2+3 = 5 is the 5th term

3+5 = 8 is the 6th term

5+8 = 13 is the 7th term

8+13 = 21 is the 8th term

This process continues until infinity, we want a function that returns the nth term of the Fibonacci sequence.

Above have our function fib, which takes in n as an input, and we immediately define our base case which is anything less than 2, as it returns 1. Now lets define our recursive case, which is anything greater than two.

Our base case is fib (n-1) + (n-2) this is derived from the Fibonacci formulae, in the example, above I have 5 which will be substituted in the place of n.

Python starts and checks are 5 less than or equal to 2, we know 5 is greater than 2 and we will move on to the else statement and substitutes 5 into n.

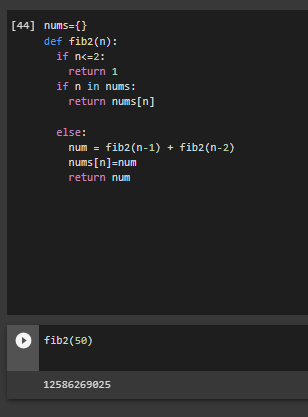
Let's experiment a little and run fib(50) a higher number and see how quick Python will be.

Referring to the image above our machine is still processing and will continue for the next hour, this is due to multiple substitutions.

Which brings us to our next question how can we make it faster? One way is using a method known as memorization, which is used to optimize the performance of functions.

As our case is special I think the use of a dictionary data structure is needed, this stores values that have already been calculated.

Instead of us sending Python to compute everything including values that have already been calculated.

We have renamed our function to fib2(to illustrate the changes), above our function we have our dictionary named nums.

Now our program checks if the value is less than 2, and if not it begins the recursive function, with the dictionary to store all values that have already been calculated.